§22. Прямоугольный параллелепипед. Пирамида - cтраницы 93, 94, 95, 96, 97, 98, 99
ПОВТОРЯЕМ ТЕОРИЮ
260. Заполните теорию.
1) Каждая грань прямоугольного параллелепипеда является прямоугольником.
2) Сторона граней прямоугольного параллелепипеда называют ребрами, вершины граней - вершинами прямоугольного параллелепипеда.
3) У параллелепипеда 6 граней, 12 ребер, 8 вершин.
4) Грани прямоугольного параллелепипеда, не имеющие общих вершин, называют противолежащими.
5) Противолежащие грани прямоугольного параллелепипеда равны.
6) Площадью поверхности параллелепипеда называют сумму площадей его граней.
7) Длины трех ребер прямоугольного параллелепипеда, имеющих общую вершину, называют измерениями прямоугольного параллелепипеда.
8) Чтобы различать измерения прямоугольного параллелепипеда, пользуюятся названиями: длина, ширина и высота.
9) Кубом называют прямоугольный параллелепипед, у которого все измерения равны.
10) Поверхность куба состоит из шести равных квадратов.
260. Заполните теорию.
1) Каждая грань прямоугольного параллелепипеда является прямоугольником.
2) Сторона граней прямоугольного параллелепипеда называют ребрами, вершины граней - вершинами прямоугольного параллелепипеда.
3) У параллелепипеда 6 граней, 12 ребер, 8 вершин.
4) Грани прямоугольного параллелепипеда, не имеющие общих вершин, называют противолежащими.
5) Противолежащие грани прямоугольного параллелепипеда равны.
6) Площадью поверхности параллелепипеда называют сумму площадей его граней.
7) Длины трех ребер прямоугольного параллелепипеда, имеющих общую вершину, называют измерениями прямоугольного параллелепипеда.
8) Чтобы различать измерения прямоугольного параллелепипеда, пользуюятся названиями: длина, ширина и высота.
9) Кубом называют прямоугольный параллелепипед, у которого все измерения равны.
10) Поверхность куба состоит из шести равных квадратов.
РЕШАЕМ ЗАДАЧИ
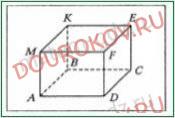
261. На рисунке изображен прямоугольный параллелепипед ABCDMKEF. Заполните пропуски.
1) Вершина В принадлежит граням АМКВ, АВСD, КВСЕ.
2) Ребру ЕF равны ребра КМ, АВ, СD.
3) Верхняя грань параллелепипеда - прямоугольник МКЕF.
4) Ребро DF является общим ребром граней АМFD и FЕСD.
5) Грани АМКВ равна грань FЕСD.
261. На рисунке изображен прямоугольный параллелепипед ABCDMKEF. Заполните пропуски.
1) Вершина В принадлежит граням АМКВ, АВСD, КВСЕ.
2) Ребру ЕF равны ребра КМ, АВ, СD.
3) Верхняя грань параллелепипеда - прямоугольник МКЕF.
4) Ребро DF является общим ребром граней АМFD и FЕСD.
5) Грани АМКВ равна грань FЕСD.
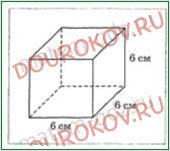
262. Вычислите площадь поверхности куба и ребром 6 см.
Решение:
Площадь одной грани равна
62-6*6 = 36 (см2)
Площадь повехности равна
6*36 = 216 (см2)
Ответ: Площадь поверхности равна 216 см2.
Решение:
Площадь одной грани равна
62-6*6 = 36 (см2)
Площадь повехности равна
6*36 = 216 (см2)
Ответ: Площадь поверхности равна 216 см2.
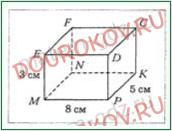
263. На рисунке изображен прямоугольный параллелепипед MNKPEFCD, измерения которого равны 8 см, 5 см и 3 см. Вычислите сумму длин всех его ребер и площадь поверхности.
Решение:
Сумма ребер
4*(8+5+3) = 64 (см)
Площадь поверхности равна:
2*(8*3+8*5+5*3) = 158 (см2)
Ответ: сумма длин всех его ребер равна 64 см, площадь поверхности - 158 см2.
Решение:
Сумма ребер
4*(8+5+3) = 64 (см)
Площадь поверхности равна:
2*(8*3+8*5+5*3) = 158 (см2)
Ответ: сумма длин всех его ребер равна 64 см, площадь поверхности - 158 см2.
264. Заполните пропуски.
1) Поверхность пирамиды состоит из боковых граней - треугольников, имеющих общую вершину и основание.
2) Общую вершину боковых граней называют вершиной пирамиды.
3) Стороны основания пирамиды называют ребрами основания, а стороны боковых граней, не принадлежащие основанию, - боковыми ребрами.
1) Поверхность пирамиды состоит из боковых граней - треугольников, имеющих общую вершину и основание.
2) Общую вершину боковых граней называют вершиной пирамиды.
3) Стороны основания пирамиды называют ребрами основания, а стороны боковых граней, не принадлежащие основанию, - боковыми ребрами.
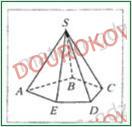
265. На рисунке изображена пирамида SABCDE. Заполните пропуски.
1) На рисунке изображена 5 угольная пирамида.
2) Боковыми гранями пирамиды являются треугольники SAB, SBC, SCD, SDE, SEA, а основанием - 5 угольник, ABCDE.
3) Вершиной пирамиды является точка S.
4) Ребрами основания пирамиды являются отрезки AB, BC, CD, DE, EA, боковыми ребрами - отрезки SA, SB, SC, SD, SE.
1) На рисунке изображена 5 угольная пирамида.
2) Боковыми гранями пирамиды являются треугольники SAB, SBC, SCD, SDE, SEA, а основанием - 5 угольник, ABCDE.
3) Вершиной пирамиды является точка S.
4) Ребрами основания пирамиды являются отрезки AB, BC, CD, DE, EA, боковыми ребрами - отрезки SA, SB, SC, SD, SE.
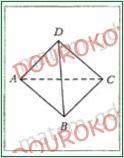
266. На рисунке изображена пирамида DАВС.ю все грани которой - равносторонние треугольники со сторонами по 4 см. Чему равна сумма длин всех ребер пирамиды?
Решение:
Сумма длин ребер равна
6*4 = 24 (см)
Ответ: 24 см.
Решение:
Сумма длин ребер равна
6*4 = 24 (см)
Ответ: 24 см.
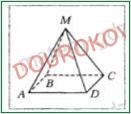
267. На рисунке изображена пирамида МАВСD, боковые грани которой - равнобедренные треугольники с боковыми сторонами по 7 см, а основание - квадрат со стороной 8 см. Чему равна сумма длин всех ребер пирамиды?
Решение:
Сумма длин боковых ребер равна
4*7 = 28 (см)
Сумма длин ребер основания равна
4*8 = 32 (см)
Сумма длин всех ребер
28+32 = 60 (см)
Ответ: сумма длин всех ребер пирамиды равна 60 см.
Решение:
Сумма длин боковых ребер равна
4*7 = 28 (см)
Сумма длин ребер основания равна
4*8 = 32 (см)
Сумма длин всех ребер
28+32 = 60 (см)
Ответ: сумма длин всех ребер пирамиды равна 60 см.
268. Может ли иметь (да, нет) форму прямоугольного параллелепипеда:
1) яблоко; 2) коробка; 3) торт; 4) дерево; 5) кусок сыра; 6) кусок мыла?
Ответ: 1) нет; 2) да; 3) да; 4) нет; 5) да; 6) да.
1) яблоко; 2) коробка; 3) торт; 4) дерево; 5) кусок сыра; 6) кусок мыла?
Ответ: 1) нет; 2) да; 3) да; 4) нет; 5) да; 6) да.
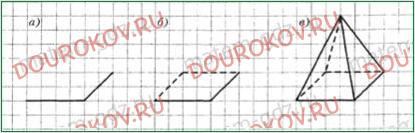
269. На рисунке показана последовательность шагов изображения прямоугольного параллелепипеда. Начертите так же параллелепипед.
271. Чему равно ребро куба, если площадь его поверхности равна 96 см2.
Решение:
1) 96:6 = 16 (см2) - площадь одной грани куба.
2) 4*4 = 16, значит ребро куба равна 4 см.
Ответ: 4 см.
Решение:
1) 96:6 = 16 (см2) - площадь одной грани куба.
2) 4*4 = 16, значит ребро куба равна 4 см.
Ответ: 4 см.
272. Запишите формулу для вычисления площади S поверхности:
1) куба, ребро которого равно а;
2) прямоугольного параллелепипеда, измерения которого равны а, b, c.
Ответ: 1) S = 6а2; 2) S = 2( аb+ас+bс)
1) куба, ребро которого равно а;
2) прямоугольного параллелепипеда, измерения которого равны а, b, c.
Ответ: 1) S = 6а2; 2) S = 2( аb+ас+bс)
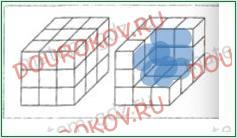
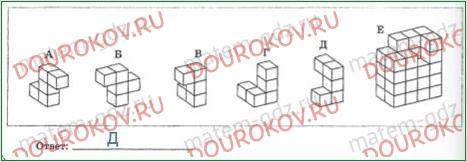
273. Для покраски куба, изображенного на рисунке слева, требуется 270 г краски. Часть куба вырезали. Сколько потребуется граммов краски, чтобы покрасить часть поверхности полученного тела, выделенную голубым цветом.
Решение:
1) 270:6:9 = 45:9 = 5 (г) - на покраску единичной грани
2) 5*12 = 60 (г) - на покраску голубой поверхности
Ответ: потребуется 60 г раски
Решение:
1) 270:6:9 = 45:9 = 5 (г) - на покраску единичной грани
2) 5*12 = 60 (г) - на покраску голубой поверхности
Ответ: потребуется 60 г раски
275. Прямоугольный параллелепипед и куб имеют равные площади поверхности. Высота параллелепипеда равна 4 см, что в 3 раза меньше его длины и на 5 см меньше его ширины. Найдите ребро куба.
Решение:
1) 4*3 = 12 (см) длина переллелепипеда
2) 4+5 = 9 (см) ширина параллелепипеда
3) 2*(4*12+4*9+12*9) = 384 (см2) площадь поверхности параллелепипеда
4) 384:6 = 64 (см2) площадь грани куба
5) 64 = 8*8 = 82, значит ребро куба 8 см.
Ответ: ребро куба 8 см.
Решение:
1) 4*3 = 12 (см) длина переллелепипеда
2) 4+5 = 9 (см) ширина параллелепипеда
3) 2*(4*12+4*9+12*9) = 384 (см2) площадь поверхности параллелепипеда
4) 384:6 = 64 (см2) площадь грани куба
5) 64 = 8*8 = 82, значит ребро куба 8 см.
Ответ: ребро куба 8 см.
276. Обведите на изображении куба цветным карандашом видимые ребра так, чтобы куб был виден: 1) сверху и справа; 2) снизу и слева.
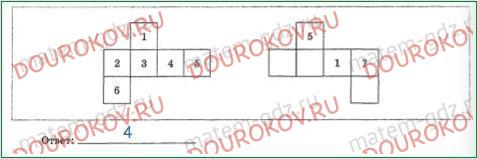
277. Грани куба пронумерованы числами от 1 до 6. На рисунке изображены два варианта развертки отдного и того же куба, полученные при равном разрезании. Какое число должно стоять вместо знака вопроса?
§21. Площадь. Площадь прямоугольника - стр. 87-92§23. Объём прямоугольного параллелепипеда - стр. 100-105
Сохраните или поделитесь с одноклассниками: