§23. Объём прямоугольного параллелепипеда - cтраницы 100, 101, 102, 103, 104, 105
ПОВТОРЯЕМ ТЕОРИЮ
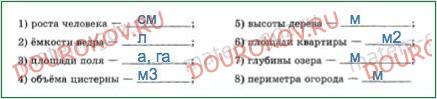
278. Заполните пропуски.
1) Равные фигуры имеют равные объемы.
2) Объем фигуры равен сумме объемов фигур, из которых она состоит.
3) За единицу измерения объема выбирают куб, ребро которого равно единичному отрезку, такой куб называют единичным.
4) Объем куба с ребром 1 мм называют кубическим миллиметром.
5) Объем куба с ребром 1 см называют кубическим сантиметром.
6) Объем куба с ребром 1 дм называют кубическим децеиметром.
7) При измерении объемов жидкостей и газов 1 дм3 называют литром.
8) Объем куба с ребром 1 м называют кубическим метром.
9) Измерить объем фигуры - значит посчитать, сколько единичных кубов в ней помещается.
10) Объем прямоугольного параллелепипеда равен произведению трех его измерений.
11) Объем прямоугольного параллелепипеда вычисляют по формуле: V = abc, V - объем, a, b, c - его измерения.
12) Объем прямоугольного параллелепипеда равен произведению площади основания на высоту.
13) Объем прямоугольного параллелепипеда вычисляют по формуле: V=Sh, где V - его объем, S - площадь основания, h - высота.
14) Объем куба вычисляют по формуле: V=а3 , где V - объем, а - длина его ребра.
278. Заполните пропуски.
1) Равные фигуры имеют равные объемы.
2) Объем фигуры равен сумме объемов фигур, из которых она состоит.
3) За единицу измерения объема выбирают куб, ребро которого равно единичному отрезку, такой куб называют единичным.
4) Объем куба с ребром 1 мм называют кубическим миллиметром.
5) Объем куба с ребром 1 см называют кубическим сантиметром.
6) Объем куба с ребром 1 дм называют кубическим децеиметром.
7) При измерении объемов жидкостей и газов 1 дм3 называют литром.
8) Объем куба с ребром 1 м называют кубическим метром.
9) Измерить объем фигуры - значит посчитать, сколько единичных кубов в ней помещается.
10) Объем прямоугольного параллелепипеда равен произведению трех его измерений.
11) Объем прямоугольного параллелепипеда вычисляют по формуле: V = abc, V - объем, a, b, c - его измерения.
12) Объем прямоугольного параллелепипеда равен произведению площади основания на высоту.
13) Объем прямоугольного параллелепипеда вычисляют по формуле: V=Sh, где V - его объем, S - площадь основания, h - высота.
14) Объем куба вычисляют по формуле: V=а3 , где V - объем, а - длина его ребра.
РЕШАЕМ ЗАДАЧИ
279. Запишите единицу измерения, которую чаще всего применяют при определении:
279. Запишите единицу измерения, которую чаще всего применяют при определении:
280. Заполните таблицу.
| 1 дм = 10 см | 1 дм2 = 100 см2 | 1 дм3 = 1000 см3 |
| 1 м = 10 дм | 1 м2 = 100 дм2 | 1 м3 = 1000 дм3 |
| 1 м = 100 см | 1 м2 = 10000 см2 | 1 м3 = 1000000 см3 |
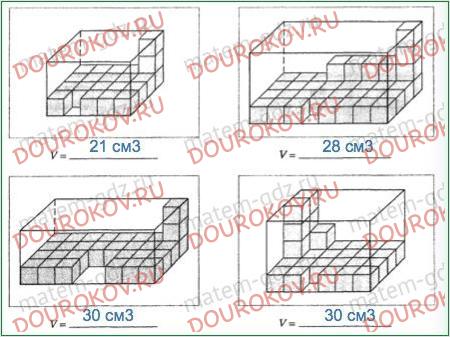
281. Фигуры, изображенные на рисунке, составлены из кубиков с ребкром 1 см. Найти объем каждой фигуры.
282. Если прямоугольный параллелепипед имеет измерения 2 дм, 4 дм и 5 дм, то его объем V=2*4*5 = 40 (дм3).
283. Если ребро куба равно 3 см, то его объем V=33 = 27 (см3).
284. Чтобы сложить прямоугольный параллелепипед, измерения которого равны 3 дм, 4 дм и 5 дм, нужно 60 кубиков с ебром 10 см.
285. Объем прямоугольного параллелепипеда равен 1080 см3, его длина - 24 см, высота - 9 см. Найдите ширину данного параллелепипеда.
Решение:
1080:24:9 = 5 (см)
Ответ: ширина параллелепипеда равна 5 см.
Решение:
1080:24:9 = 5 (см)
Ответ: ширина параллелепипеда равна 5 см.
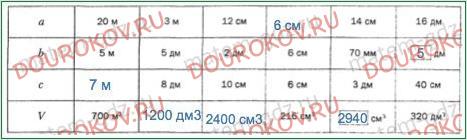
286. Заполните таблицу, где V - объем прямоугольного параллелепипеда, a, b, c - его измерения.
1) 700:20:5 = 7 (м)
2) 30*5*8 = 1200 (дм3)
3) 12*20*10 = 2400 (см3)
4) 216:6:6 = 6 (см)
5) 140*70*300 = 2940000 (мм3) = 2940 (см3)
6) 320:16:4 = 5 (дм)
1) 700:20:5 = 7 (м)
2) 30*5*8 = 1200 (дм3)
3) 12*20*10 = 2400 (см3)
4) 216:6:6 = 6 (см)
5) 140*70*300 = 2940000 (мм3) = 2940 (см3)
6) 320:16:4 = 5 (дм)
287. Площадь поверхности куба равна 150 см3. Найдите объем этого куба.
Решение:
1) 150:6 = 25 (см2) - площадь грани куба
2) 25 = 52, т.е. ребро куба 5 см
3) 53 = 125 (см3) - объем куба
Ответ: 125 см3.
Решение:
1) 150:6 = 25 (см2) - площадь грани куба
2) 25 = 52, т.е. ребро куба 5 см
3) 53 = 125 (см3) - объем куба
Ответ: 125 см3.
288. Сравните величины.
289. Заполните пропуски.
290. За сутки человек делает вдох-выдох приблизительно 22500 раз. За один вдох в легкие попадает 400 см3 воздуха. Сколько литров воздуха проходит через легкие человека за сутки?
Решение:
22500*400 = 9000000 (см3) = 9000 (л)
1 л = 1000 см3
Ответ: 9000 л.
Решение:
22500*400 = 9000000 (см3) = 9000 (л)
1 л = 1000 см3
Ответ: 9000 л.
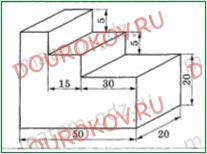
291. Вычислите объем фигуры, изображенной на рисунке (размеры считать в см).
Решение:
V = 20*(50*20+(50-30)*5+(50-30-15)*5) = 20*(1000+100+25) = 20*1125 = 22500 (см3).
Ответ: 22500 см3.
Решение:
V = 20*(50*20+(50-30)*5+(50-30-15)*5) = 20*(1000+100+25) = 20*1125 = 22500 (см3).
Ответ: 22500 см3.
292. В пустой аквариум, длина котрого равна 80 см, а ширина - 40 см, налили 18 ведер воды, а каждом из которых было 10 л воды. Определите расстояние от поверхности воды до дна аквариума.
Решение:
1) 80*40 = 3200 (см2) площадь дна аквариума
2) 18*10000 = 180000 (см3) объем налитой воды
3) 180000:3200 = 1800:32 = 56 ост.25 (см) от поверхности воды до дна аквариума
Ответ: 56 ост.25
Решение:
1) 80*40 = 3200 (см2) площадь дна аквариума
2) 18*10000 = 180000 (см3) объем налитой воды
3) 180000:3200 = 1800:32 = 56 ост.25 (см) от поверхности воды до дна аквариума
Ответ: 56 ост.25
293. Ребро одного куба в 5 раз больше ребра другого. Во сколько раз: 1) площадь поверхности первого куба больше площади поверхности второго; 2) объем первого куба больше объема второго?
Решение:
1) S1 = S2 = 6*(5a)2:(6*a2) = 25
2) V1 = V2 = (5a)3:a3 = 125
Ответ: 1) в 25 раз; 2) в 125 раз.
Решение:
1) S1 = S2 = 6*(5a)2:(6*a2) = 25
2) V1 = V2 = (5a)3:a3 = 125
Ответ: 1) в 25 раз; 2) в 125 раз.
294. Если ребро куба уменьшить в 6 раз, то его объем уменьшится в 216 раз.
295. Если длину прямоугольного параллелепипеда увеличить в 7 раз, ширину - в 3 раза, а высоту - в 2 раза, то его объем увеличится в 42 раза.
Сохраните или поделитесь с одноклассниками: