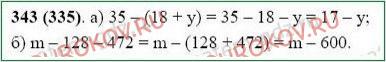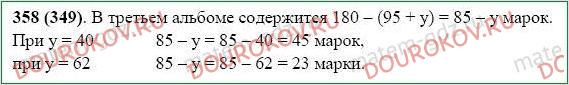9. Буквенная запись свойств сложения и вычитания - cтраницы 54, 55, 56, 57, 58
337. Запишите сочетательное свойство сложения с помощью букв a, b и с. Замените буквы их значениями: а = 9873, b = 6914, с = 10 209 – и проверьте получившееся числовое равенство.
338. Запишите свойство вычитания суммы из числа с помощью букв a, b и с. Замените буквы их значениями: а = 243, b = 152, c = 88 – и проверьте получившееся числовое равенство.
339. Запишите свойство вычитания числа из суммы двумя способами. Проверьте получившиеся числовые равенства, заменив буквы их значениями:
а) а = 98, b = 47 с = 58;
б) а = 93, b = 97 и с = 95.
а) а = 98, b = 47 с = 58;
б) а = 93, b = 97 и с = 95.
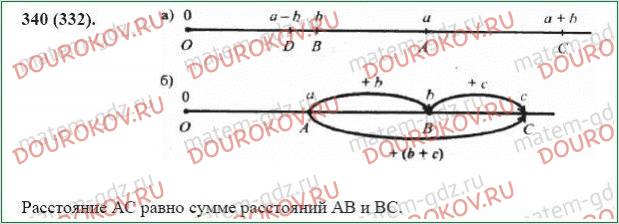
340. а) На рисунке 42 с помощью циркуля найдите точки М(a + b) и N(a – b).
б) Объясните по рисунку 43 смысл сочетательного свойства сложения.
в) Объясните с помощью рисунков остальные свойства сложения и вычитания.
б) Объясните по рисунку 43 смысл сочетательного свойства сложения.
в) Объясните с помощью рисунков остальные свойства сложения и вычитания.
341. Из свойств сложения следует:
56 + х + 14 = х + 56 + 14 = х + (56 + 14) = х + 70.
По этому образцу упростите выражение:
56 + х + 14 = х + 56 + 14 = х + (56 + 14) = х + 70.
По этому образцу упростите выражение:
343. Из свойств вычитания следует:
28 – (15 + с) = 28 – 15 – с = 13 – с,
а – 64 – 26 = а – (64 + 26) = а – 90.
Какое свойство вычитания применено в данных примерах?
Используя это свойство вычитания, упростите выражение:
28 – (15 + с) = 28 – 15 – с = 13 – с,
а – 64 – 26 = а – (64 + 26) = а – 90.
Какое свойство вычитания применено в данных примерах?
Используя это свойство вычитания, упростите выражение:
344. Из свойств сложения и вычитания следует:
137 – с – 27 = 137 – (с + 27) = 137 – (27 + с) = 137 – 27 – с = 110 – с.
Какие свойства сложения и вычитания применены в этом примере? Используя эти свойства, упростите выражение:
137 – с – 27 = 137 – (с + 27) = 137 – (27 + с) = 137 – 27 – с = 110 – с.
Какие свойства сложения и вычитания применены в этом примере? Используя эти свойства, упростите выражение:
345. Из свойств вычитания следует:
(154 + b) – 24 = (154 - 24) + b = 130 + b;
а – 10 + 15 = (а – 10) + 15 = (а + 15) – 10 = а + (15 - 10) = а + 5.
Какое свойство вычитания применяется в этом примере?
Используя это свойство, упростите выражение:
(154 + b) – 24 = (154 - 24) + b = 130 + b;
а – 10 + 15 = (а – 10) + 15 = (а + 15) – 10 = а + (15 - 10) = а + 5.
Какое свойство вычитания применяется в этом примере?
Используя это свойство, упростите выражение:
347. На отрезке АВ отмечены точки C и D, причем точка С лежит между точками A и D. Составьте выражение для длины отрезка:
а) АВ, если АС = 453 мм, CD = х мм и DB = 65 мм. Найдите значение получившегося выражения при х = 315; 283.
б) АС, если АВ = 214 мм, CD = 84 мм и DB = у мм. Найдите значение получившегося выражения при у = 28; 95.
а) АВ, если АС = 453 мм, CD = х мм и DB = 65 мм. Найдите значение получившегося выражения при х = 315; 283.
б) АС, если АВ = 214 мм, CD = 84 мм и DB = у мм. Найдите значение получившегося выражения при у = 28; 95.
348. Токарь выполнил заказ на изготовление одинаковых деталей за три дня. В первый день он изготовил 23 детали, во второй день – на b деталей больше, чем в первый день, а в третий день – на четыре детали меньше, чем в первый день. Сколько деталей изготовил токарь за эти три дня? Составьте выражение для решения задачи и найдите его значение при b = 7, b = 9.
351. Придумайте задачу, решением которой является выражение:
а) (47 - 15) + (62 - 12);
б) х + (39 - 14);
в) 81 – (х + у).
а) (47 - 15) + (62 - 12);
б) х + (39 - 14);
в) 81 – (х + у).
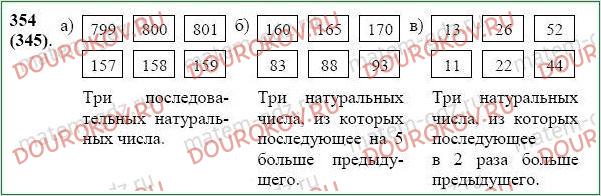
353. Как изменится сумма, если:
а) одно из слагаемых увеличить на 5;
б) одно слагаемое увеличить на 5, а второе – на 10;
в) одно слагаемое увеличить на 6, а второе уменьшить на 6;
г) одно из слагаемых увеличить вдвое?
а) одно из слагаемых увеличить на 5;
б) одно слагаемое увеличить на 5, а второе – на 10;
в) одно слагаемое увеличить на 6, а второе уменьшить на 6;
г) одно из слагаемых увеличить вдвое?
356. Сколько двузначных чисел можно составить из цифр 1, 3, 5, 7, 9, если цифры в записи числа не повторяются?
Сколько трехзначных чисел можно составить из тех же цифр (цифры в записи числа не повторяются)?
Сколько трехзначных чисел можно составить из тех же цифр (цифры в записи числа не повторяются)?
357. Найдите площадь двухкомнатной квартиры, если площадь обеих комнат 35 м², площадь кухни 9 м², а подсобные помещения имеют общую площадь а м². Составьте выражение для решения задачи и найдите его значение при а = 8 и а = 12.
358. У Пети 180 марок в трех альбомах. В одном альбоме 95 марок, а в другом у марок. Сколько марок у Пети в третьем альбоме? Составьте выражение для решения задачи и найдите его значение при у = 40; 45; 62.
359. В сарае было 138 т сена. В первый месяц израсходовали 49 т сена, а во второй месяц – на х т больше. Сколько тонн сена осталось в сарае? Составьте выражение для решения задачи и найдите его значение при х = 14; 20; 30.
362. По дороге движутся навстречу друг другу пешеход и велосипедист. Сейчас расстояние между ними 52 км. Скорость пешехода 4 км/ч, а скорость велосипедиста 9 км/ч. Какое расстояние будет между ними через 1 ч; через 2 ч; через 4 ч? Через сколько часов пешеход и велосипедист встретятся?
366. Мотогонщик преодолел первый участок трассы за 54 с, второй – за 46 с, а третий – на n с быстрее, чем второй. Сколько времени затратил мотогонщик на прохождение этих трех участков? Найдите значение полученного выражения, если n = 9; 17; 22.
367. В треугольнике одна сторона 36 см, другая на 4 см меньше, а третья на х см больше первой стороны. Найдите периметр треугольника. Составьте выражение для решения задачи и найдите его значение при х = 4 и х = 8.
368. Турист на автобусе проехал 40 км, что в 5 раз больше того пути, который он прошел пешком. Какой общий путь проделал турист?
369. От города до села 24 км. Из города вышел человек и идет со скоростью 6 км/ч. Изобразите на шкале расстояний (одно деление шкалы – 1 км) положение пешехода через 1 ч после выхода из города; через 2 ч; через 3 ч и т. д. Когда придет он в село?
Сохраните или поделитесь с одноклассниками: